Edge-preserving noise for diffusion models

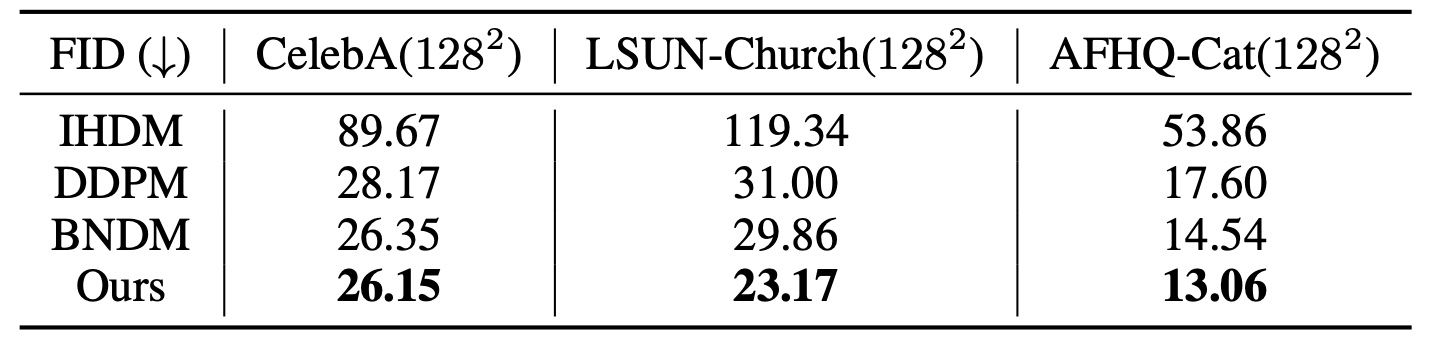
Classical generative diffusion models learn an isotropic Gaussian denoising process, treating all spatial regions uniformly, thus neglecting potentially valuable structural information in the data. Inspired by the long-established work on anisotropic diffusion in image processing, we present a novel edge-preserving diffusion model that is a generalization of denoising diffusion probablistic models (DDPM). In particular, we introduce an edge-aware noise scheduler that varies between edgepreserving and isotropic Gaussian noise. We show that our model’s generative process converges faster to results that more closely match the target distribution. We demonstrate its capability to better learn the low-to-mid frequencies within the dataset, which plays a crucial role in representing shapes and structural information. Our edge-preserving diffusion process consistently outperforms state-of-the-art baselines in unconditional image generation. It is also more robust for generative tasks guided by a shape-based prior, such as stroke-to-image generation. We present qualitative and quantitative results showing consistent improvements (FID score) of up to 30% for both tasks.

We propose a hybrid diffusion process that starts out by suppressing noise on edges, better preserving structural details of the underlying content. Halfway through the process, we switch over to isotropic white noise, to ensure that we converge to a prior distribution from which we can analytically take samples.

Figure 1: This animation shows the difference between a classic isotropic diffusion process and our hybrid edge-preserving diffusion process.

Denoising is a technique that has been around for a long time in the field of image processing. Historically, researchers used to design convolution kernels by hand to do this. A naive way of noise removal is in an isotropic manner, which blurs the image in a spatially-uniform manner regardless of its underlying content. As a consequence, the noise is reduced but the important structural information in the image is also lost. Researchers saw that it instead was much more effective to do the denoising in an anisotropic, content-aware manner. A seminal work that demonstrates this is anisotropic diffusion [Perona and Malik, 1990].

Observe that diffusion models are also denoisers. Contrary to traditional noise removal techniques, their denoising capabilities are governed by the learned complex convolution filters in a deep neural network, which allows them to go from a distribution of pure noise to noise-free images. The idea behind this project is therefore to make diffusion models more aware of the underlying content they are denoising by proposing a content-aware noise.

We demonstrate that our content-aware diffusion process brings several advantages. First of all, it improves unconditional image generation. Most remarkably, it has a positive impact on generative tasks driven by shape information, such as the example shown in Figure 2. Finally, it is able to better learn the low-to-mid frequencies in the data, which are typically responsible for structural semantic information.

Comparison between different baselines and our method applied to the SDEdit framework.

Figure 2: Left: A comparison of our diffusion model, DDPM [Ho et al. 2020] and BNDM [Huang et al. 2024] applied to the SDEdit framework [Meng et al. 2022], which uses a stroke painting as a prior for image generation. Overall our model shows sharper details with less distortions compared to other models, leading to a better visual and quantitative performance. The corresponding FID scores are shown in the top of the right column. Right: Our model also effectively uses human-drawn paintings as shape guides, with particularly precise adherence to details, such as the orange patches on the cat’s fur, unlike DDPM (middle column).

The main idea is that we make the diffusion process explicitly aware of the underlying structural content by longer preserving the structural details and learning the non-isotropic variance that goes in hand with this. We achieve this in particular by suppressing the injected noise in areas with high image gradients, according to the formulation of anisotropic diffusion in image processing [Perona and Malik, 1990].

We propose a time-varying noise scheme that interpolates between edge-preserving and isotropic Gaussian noise. Note that it is important that we do this interpolation, given the fact that we want to end up with an easy distribution which we can analytically sample at t = T.

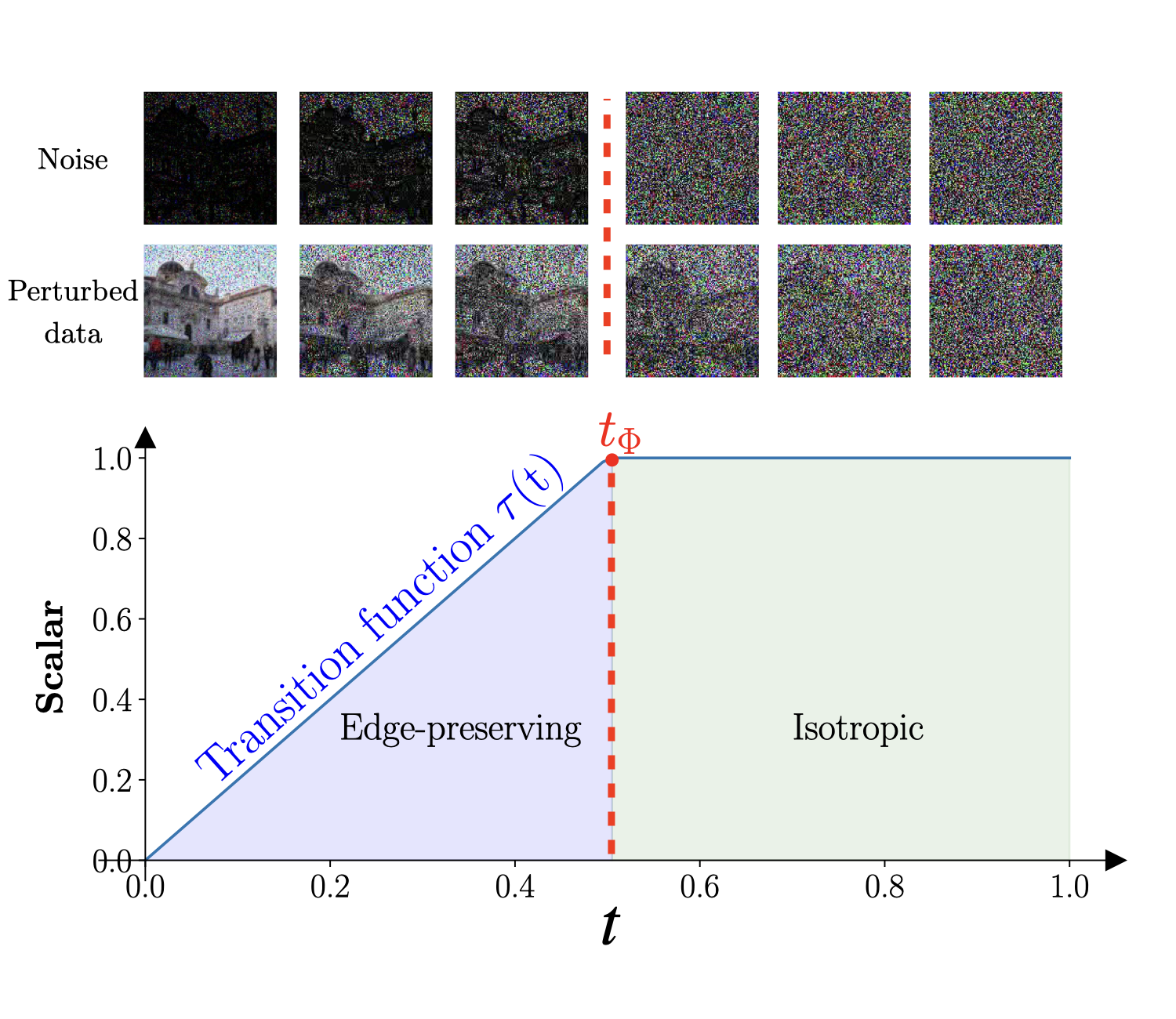
Contrary to isotropic diffusion models that learn an unscaled Gaussian white noise, our model explicitly learns the non-isotropic variance that corresponds to the edge information in the data set.

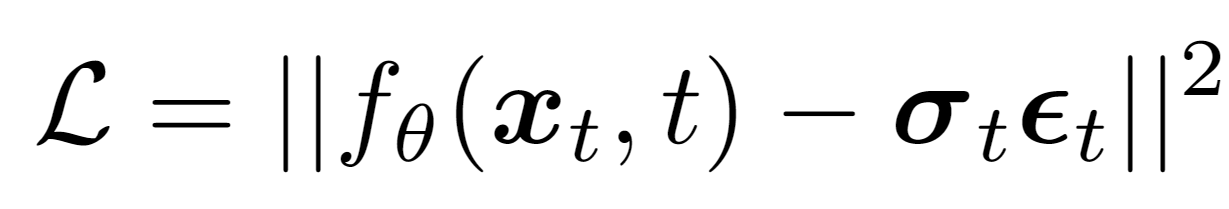
As an example, consider the image sequence below, with decreasing cutoff frequency $σ$ . We observe that the lower frequencies still represent the core structural shape information. In other words, the harder the edge, the larger the frequency span of that edge (the shapes formed by the hardest edges are still visible, even at very low frequency bands).

Since edges and their strength are closely related to shape information (represented by lower frequencies), as seen in the example above, we expect our method to impact learning those frequencies. We confirmed this through a frequency analysis comparing our model's performance to the isotropic DDPM model across different frequency bands. Our model showed better learning of low-to-mid frequencies. The figure below shows the evolution of FID scores over the first 10,000 training iterations per frequency band (larger $σ$ values indicate lower frequencies). Our model significantly outperforms DDPM in the lower and middle bands (lower FID is better).

Our proposed backward diffusion process converges faster to predictions that are sharper and less noisy. For a visual example that demonstrates this, we refer to the interactive slider below. We show the predicted image ${\hat{𝐱}}_{0}$ , together with the predicted noise mask at each time step.

Note how structural details (e.g. the pattern on the cat's head, whiskers, face contour) become visible significantly earlier for our process. Also note that our diffusion model explicitly learns the non-isotropic variance corresponding to the edge content in the data. This becomes apparent in the predicted noise mask, that shows the shape of the cat face towards the end.

${\hat{𝐱}}_{0}$ at t = T (DDPM)

${\hat{𝐱}}_{0}$ at t = 0 (DDPM)

${\hat{𝐱}}_{0}$ at t = T (Ours)

${\hat{𝐱}}_{0}$ at t = 0 (Ours)

In addition to the results in the main paper, we provide videos of the unconditional generative sampling process for IHDM, BNDM, DDPM and Ours trained on different datasets.

Results for the Human Sketch (128x128) dataset.

Figure 4: Selected samples for the Human Sketch (128x128) dataset [Eitz et al. 2012]. This dataset was of particular interest to us, given the images only consist of high-frequency, edge content. Although we observed that this data is remarkably challenging for all models, our method is able to consistently deliver visually better results.

BibTeX

@article{vandersanden2024edge,
  author    = {Vandersanden, Jente and Holl, Sascha and Huang, Xingchang and Singh, Gurprit},
  title     = {Edge-preserving noise for diffusion models},
  journal   = {arXiv},
  year      = {2024},
}

Edge-preserving noise for diffusion models

Abstract

A hybrid content-aware diffusion process

Why edge-preserving noise?

How it works

Low-to-mid frequencies of target data

Backward generative process

Additional results

↓ Comparison of unconditional sampling process for different models pre-trained on AFHQ-Cat (128x128)

↓ Comparison of unconditional sampling process for different models pre-trained on CelebA (128x128)

↓ Comparison of unconditional sampling process for different models pre-trained on LSUN-Church (128x128)

↓ Comparison on Human Sketch (128x128) dataset between IHDM, BNDM, DDPM and Ours.

Related work

BibTeX